Podstawy Programowania - Ćwiczenia 6

Zasady, Ćw1, Ćw2, Ćw3, Ćw4, Ćw5, Ćw6, Ćw7, Ćw8, Ćw9, Ćw10, Ćw11, Ćw12, Ćw13

Prowadzący: Rafał Witkowski
Temat: Rekurencja, wskaźniki, drzewa binarne.

Rekurencja

Charakterystyczną cechą funkcji (procedury) rekurencyjnej jest to, że wywołuje ona samą siebie. Drugą cechą rekursji jest jej dziedzina, którą mogą być tylko liczby naturalne.
Funkcja rekurencyjna przeważnie opiera się na pewnym wzorze, w którym po obu stronach równości występuje ta sama funckja obliczana dla różnej wielkości parametru. Oprócz tego w każdej funkcji rekurencyjnej niezbędny jest tzw. "warunek początkowy", dzięki któremu wartość funkcji można obliczyć.
Najłatwiej zrozumieć mechanizm działania rekursji na przykładzie silni.

Silnia

Matematyczna definicja silni wygląda następująco:

$n!=\begin{cases} 1 & \mbox{ dla }n=0 \\ n(n-1)! & \mbox{ dla }n\ge1 \end{cases}$
Jak widać, silnia zdefiniowana jest niemal przez samą siebie. Do tego mamy zdefiniowany warunek początkowy: 0! = 1;
Czyli aby obliczyć 4! trzeba najpierw obliczyć 3! i wynik pomnożyć przez 4. Żeby obliczyć 3! trzeba obliczyć 2!. Żeby z kolei to obliczyć trzeba znać 1!, do obliczenia którego jest potrzebne 0!, którą to liczbę znamy, bo jest nią 1. Zatem teraz cofając się z tym rozumowaniem i podstawiając kolejne wartości mamy:
1! = 1*1 = 1;
2! = 2*1! = 2*1 = 2; 3! = 3*2! = 3*2 = 6; 4! = 4*3! = 4*6 = 24;

Zadanie 1

zadanie ppr10

Rekurencja c.d.

Funkcje rekurencyjną często można zamienić na zwykłą funkcję iteracyjną. Np. w przypadku silni oczywiście wiemy, że n! = n(n-1)(n-2)...2*1. Można to łatwo wyliczyć przy pomocy zwykłej pętli. I jeśli tylko można należy rekurencji unikać, gdyż funkcje rekurencyjne mają dużą złożoność obliczeniową, a ponad to wymagają zastosowania wewnętrznego stosu.
Niemniej często nie da się zrobić czegoś bez rekurencji, więc jest na narzędzie bardzo przydatne, które warto znać.

Wskaźniki

Szczegółowe informacje o wskaźnikach pojawiły się w sposób wyczerpujacy na wykładzie.

Drzewa binarne

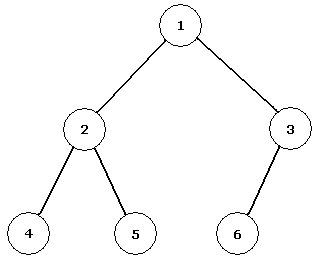
Drzewo binarne to taka struktura danych, które składa się z poziomów, na których umieszczone są wierzchołki i krawędzi, króre łączą wierzchołki z sąsiednich poziomów w taki sposób, że wierzchołek z poziomu wyższego ma co najwyżej dwóch sąsiadów na poziomie niższym. Ci sąsiedzi zą nazywani jego "lewym" i "prawym synem". Na poziomie pierwszym (najwyższym) znajduje się zawsze tylko jeden wierzchołek, który nazywany jest korzeniem drzewa. Przykładowe drzewo widać na rysunku poniżej:

Jeśli w drzewie takim wprowadzimy zasadę, że lewy syn jest zawsze mniejszy od swojego ojca, a prawy syn zawsze od niego mniejszy, można w łatwy sposób przy pomocy takiego drzewa sortować ciągi liczb.

Zadanie 2

Popraw poniższy fragment rozwiązania zadania ppr11, oraz dopisz brakującą procedurę:

#include <stdio.h>

struct w	\\ deklaracja struktury, w której przechowywane będą wierzchołki drzewa
{
  char naz;	\\ nazwa zawodnika
  int licz;	\\ liczba punktów zawodnika
  w* l;		\\ wskaźnik na lewego syna wierzchołka
  w* r;		\\ wskaźnik na prawego syna wierzchołka
};

int d,q,i,n,k;
char c;
w korzen;	\\ zmienna określająca korzeń drzewa

void do_drzewa(w * p, int x, char y)	
{		\\ procedura rekurencyjna dodająca nowy wierzchołek do drzewa
		\\ p - wierzchołek, do którego w chwili obecnej próbujemy dodać nowy wierzchołek
		\\ x, y - liczba punktów i nazwa zawodnika, którego dodajemy
  w* q;		\\ q - wierzchołek pomocniczy
  if (p==NULL)  \\ jeśli wierzchołek, do któego dodajemy jest pusty, to musimy go dopiero założyć
  {
    p = new w;
    p->licz = x;
    p->naz = y;
    p->l = NULL;
    p->r = NULL;
  } else	\\ jeśli wierzchołek juz istnieje, wówczas...
  {
    if (x<p->licz)	\\ ... jeśli liczba punktów nowego wierzchołka jest mniejsza od dodawanego...
      if (p->l == NULL) \\ ... zaglądamy, czy jest już lewy sąsiad tego wierzchołka. Jeśli nie ma (jest NULL)
      {			\\ ... to dodamy po lewej stronie nowy wierzchołek
        q = new w;	\\ alokujemy pamięć na nomwy wierzchołek (rezerwujemy na niego miejsce w pamięci)
        q->licz = x;	\\ ten nowy wierzchołek będzie miał odpowiednią liczbę punktów...
        q->naz = y;	\\ ... i odpowiednią nazwę
        q->l = NULL;	\\ nie ma narazie lewego...
        q->r = NULL;	\\ ... ani prawego syna
        p->l = q;	\\ za to nowym lewym synem wierzchołka, do którego dodajemy jest dodawany wierzchołek
      } else	\\ jeśli wierzchołek po lewej istnieje, to...
        do_drzewa(p->l,x,y); \\ ... rekurencyjnie próbujemy do niego dodać nowy wierzchołek
    else		\\ analogicznie zachowujemy się z prawej strony
    if (p->r==NULL)
    {
      q = new w;
      q->licz = x;
      q->naz = y;
      q->l = NULL;
      q->r = NULL;
      p->r = q;
    } else
      do_drzewa(p->r,x,y);
  }
}

void wypisz(???)
{
  ???
};

int main()
{
  scanf("%d\n",&d);
  while(d--)
  {
    korzen.licz = -1;		// zaznaczamy w ten sposób, ze korzeń jest pusty (trick)
    scanf("%d\n",&n);		// liczba zawodników
    for (int i=0; i<n; i++)	// pętla
    {
      scanf("%d %c\n",&c,&k);	// sczytanie nazwy i liczby punktów zawodnika
      if (korzen.licz == -1) {	// jeśli korzeń jest pusty, to go uzupełniamy:
        korzen.l = NULL;	// nie ma narazie lewego...
        korzen.r = NULL;	// ... ani prawego syna
        korzen.licz = k;	// ustawiamy odpowiednią liczbę punktów...
        korzen.naz  = c;	// ... i nazwę pierwszego zawodnika
      } else			// jeśli korzeń nie jest już pusty...
        do_drzewa(&korzen, k, c); // ... to próbujemy do niego dodać nowy wierzchłek w drzewie
    }
    wypisz(???);
  }
  return 0;
}

Podpowiedź:
procedura dopisywania do drzewa jest napisana poprawnie.

Zadanie* 3

Przy pomocy wskaźników można zrobić także zadanie ppr9. Wystarczy zaimplementować kolejkę na wskaźnikach, a następnie oprócz pusha i popa napisać procedurę wyciągającą elementy ze środka.