5 - Rekurencja
Cele lekcji
Co powinieneś już wiedzieć?
- Jak zdefiniować i wywołać funkcję
- Jak przekazywać argumenty do funkcji
- Jak zwracać wartość z funkcji
Rekurencja
Funkcja rekurencyjna to funkcja, która wywołuje samą siebie.
Oprócz takiego wywołania funkcja rekurencyjna musi zawierać warunek stopu, dzięki któremu nie będzie wykonywana w nieskończoność.
Przykład
Dla przykładu przedstawimy funkcję rekurencyjną obliczającą wartości wyrazów ciągu Fibonacciego, określonego wzorami
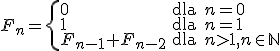
Warunkiem stopu będzie n<2. Funkcja wygląda następująco:
int F(int n)
{
if (n==0) return 0;
}
if (n==1) return 1;
return F(n-1)+F(n-2);
Rekurencja ze spamiętywaniem
Przedstawiona powyżej funkcja jest nieefektywna, ponieważ wartości wyrazów ciągu są obliczane po wiele razy. Aby uniknąć tego problemu, można zastosować rekurencję ze spamiętywaniem. Polega to na zapamiętywaniu obliczonych wartości w tablicy i sprawdzaniu, czy dana wartość jest już znana, przed wywołaniem rekurencyjnym.
Przykład dla funkcji obliczającej wyrazy ciągu Fibonacciego dla n<100 (ponieważ wyrazy ciągu dla n>1 są dodatnie, możemy oznaczać liczbą 0 te wartości, które nie zostały jeszcze obliczone):
int Ft[100]={0};
int F(int n)
{
if (n==0) return 0;
}
if (n==1) return 1;
if (Ft[n]!=0) return Ft[n];
Ft[n]=F(n-1)+F(n-2);
return Ft[n];
Zastanów się