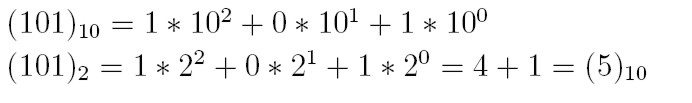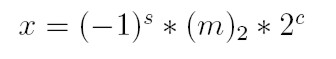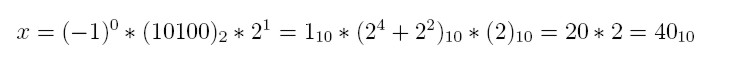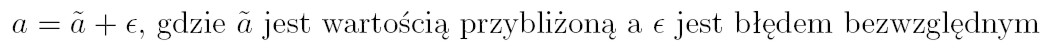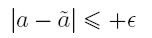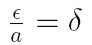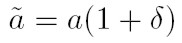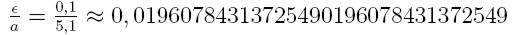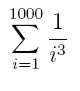W komputerze liczby zmiennopozycyjne są pamiętane w postaci
znormalizowanej. Oznacza to, że mantysa jest zawsze zapisana w postaci
znormalizowanej czyli jest liczbą postaci: 1.xxxxxxxx , a
więc 1 <= |m| < 2.
Ponieważ zawsze na początku mantysy znajduje się cyfra 1, nie zapisuje
się jej w komputerze, lecz jest tam w sposób domyślny.
UWAGA! Cecha jest zapisana tak
jak każda inna liczba całkowita w komputerze, czyli pierwszy bit
oznacza znak, a kolejne oznaczają
Zadanie 2.
Jak w komputerze wygląda liczba zmiennopozycyjna 1.0? a jak 1.5?, 0.25?
0.5? 3.0? albo 12.75?
Aby zobaczyć wynik, można skorzystać z programu:
#include <iostream>
using namespace std;
float _zmienno; // 4 bajty czyli 8*4 bitow
void bity(unsigned char* bajty, int poczatek, int koniec)
{
for (int i=koniec; i>=poczatek; i--)
{
if (i>=poczatek && i<=koniec)
{
if ((int)(*(bajty+(i/8)) )& ((1 << i%8)))
cout << 1;
else
cout << 0;
}
}
}
void liczba_binarnie(unsigned char a)
{
for (int i=7; i>=0; i--)
{
cout << (int)((a & (1 << i))>>i);
}
}
int main()
{
cout << "podaj liczbe zmiennopozycyjna: ";
cin >> _zmienno;
unsigned char *liczba = (unsigned char*) &_zmienno;
unsigned char l[4];
for (int i=0; i<4; i++)
{
printf("\nbajt %d %d (dziesietnie) ---> ", i, *(liczba+i));
liczba_binarnie(*(liczba+i));
printf("\n");
l[i]=*(liczba+i);
}
cout << endl << "znak: ";
bity(liczba, 31,31);
cout << endl << "cecha: ";
bity(liczba,23,30);
cout << " rzeczywista to zminiejszona o 127 czyli: " << ((l[3] << 1)| (l[2] >>7)) - 127 << endl;
cout << "mantysa: ";
bity(liczba, 0, 22);
cout << endl;
return 0;
}
Czy wyniki są takie jak można się było
spodziewać?
Uwaga:
Jak można zauważyć w programie (przy jego uruchomieniu) liczba cechy
przed ustaleniem dokładnego wyniku musi zostać zmniejszona. Powodem
tego jest, iż w rzeczywistości chcemy mieć możliwość zapisywania
również małych liczb ułamkowych a tylko w ten sposób możemy wymusić
taką sytuację.
Przesunięcia
E te są
różne dla różnego rodzaju typów (float, double).
Uwaga:
Jak można było zobaczyć na wynikach mantysa ma czasami dziwny wygląd
np. dla wartości 1 mantysą są same 0. Dlaczego tak jest?
Liczby zmiennopozycyjne - ilość reprezentacji.
Jak można łatwo zauważyć ilość liczb które możemy zapisać w zmiennej
zmiennopozycyjnej float lub double jest skończona i wynosi
2^ilość_bitow_liczby. Część liczb musi więc być niedokładnie
zapamiętywana - czyli przybliżana. Pytanie jak gęsto są te liczby w
rzeczywistości "upakowane" ? Załóżmy że mamy reprezentację
zmiennopozycyjną na 6 bitach: s-1bit, c-2bity, m-3
bity. Jakie liczby są dokładnie reprezentowane w tym zapisie?
Zakładamy że przesunięcie (to co w liczbach typu float wynosi
tutaj 1 czyli: ) gdy cecha = 11 to wartość = 10 czyli 2
dziesiętnie ... iid
Możliwe wartości mantysy to:
Mantysa:
Wartość binarna
|
Wartość
dziesięsiętna
|
(1,)000
|
1,000
|
(1,)001
|
1,125
|
(1,)010
|
1,250
|
(1,)011
|
1,375
|
(1,)100
|
1,500
|
(1,)101
|
1,675
|
(1,)110
|
1,750
|
(1,)111
|
1,875
|
|
Cecha:
Wartość binarna
|
Wartość
dziesiętna 2^cecha
|
00
|
0,5
|
01
|
1
|
10
|
2
|
11
|
4
|
|
|
Po wykonaniu obliczeń zauważyć można jakie liczby w rzeczywistości mogą
być reprezentowane poprzez taki format zapisu liczby.
Wykres rozwiązania wygląda następująco(gdzie kropki wskazują
reprezentowane dokładnie liczby):
Uwaga: Jak widać na wykresie
gęstość liczb w okolicach zera jest większa niż w dalszej odległości.
Jest to specyfika liczb zmiennopozycyjnych. Oczywiście w komputerach
dokładność ta jest większa ponieważ na liczbę przeznaczanych jest
więcej bitów pamięci, jednak sytuacja ta wygląda analogicznie.
Zadanie 3
Obliczyć samemu jakie wartości mogą przyjmować wszystkie liczby dla
wartości z powyższego przykładu. Czy na osi zostały zaznaczone
wszystkie możliwe liczby?
Zadanie 4
Obliczyć samemu jakie wartości mogą przyjmować wszystkie liczby, jeśli:
s-1bit, c-3bity, m-2
bity
Błąd bezwzględny
Wartość dokładna może być określona następującym wzorem:
W ten sposób zdefiniowany jest również błąd bezwzględny dla naszych
liczb zmiennopozycyjnych określa go następująca nierówność:
Bowiem załóżmy iż chcemy określić jaki błąd bezwzględny dla
reprezentacji liczby 2.34 w systemie podanym wcześniej (w pkt.
dot. ilości reprezentacji liczb zmiennopozycyjnych)
Jak można zauważyć najbliższą wartością tej liczby jest liczba 2.25. a
więc korzystając ze wzoru powyższego błąd bezwzględny jest mniejszy
niż:
|2.34-2.25| = 0.09.
Błąd względny
Błąd względny definiujemy jako:
Lub inaczej:
Mówimy iż błąd względny wyraża ilość informacji zawartej w a. Jest to
bardziej miarodajny sposób określania wielkości błędu. Bowiem na jego
podstawie jesteśmy wstanie określić jak duży błąd otrzymaliśmy w
stosunku do wielkości wyniku.
Przykład 4
Załóżmy że przybliżamy liczbę 5,1 za pomocą reprezentacji podanej
wcześniej. Liczbę tę możemy przybliżyć za pomocą wartości 5. Jaki błąd
względny i bezwzględny otrzymaliśmy dla tego przybliżenia?
Rozwiązanie:
błąd bezwzględny:

błąd względny:
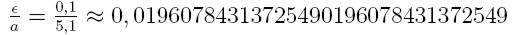
Zadanie 5
Oblicz z jakim błędem względnym i bezwzględnym mogą być zapisane
następujące liczby w komputerze:
a) 0,1 gdy s=1, c=5, m=2
b) 12,75 gdy s=1, c=3, m=4
c) 1027 gdy s=1, c=8, m=7
Błedy spowodowane reprezentacją liczb zmiennopozycyjnych
Podczas wykonywania wielu operacji matematycznych na liczbach
zmiennopozycyjnych należy pamiętać o wielu różnych właściwościach tych
liczb(jakie operacje powoduja duże, a jakie małe błędy, kolejność
sumowania liczb oraz wiele innych czynników o których będzie mowa na
kolejnych zajęciach).
Aby pokazać jak ważne jest pamiętanie o tym prosze sobie wyobrazić, iż
mamy do policzenia następujący szereg:
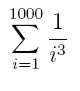
Zadanie 6 (zad. domowe)
Napisz program liczący taką sumę
najpierw "od dołu", a później "od góry".
Czyli
Jakie wyniki otrzymano po wykonaniu takiego programu? Jak myślisz -
dlaczego ???