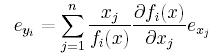

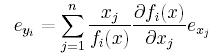
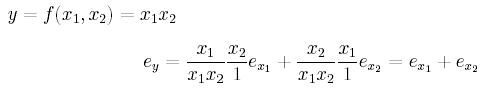
program niesk;Który wynik jest obarczony mniejszym błędem? Dlaczego?
{$APPTYPE CONSOLE}
var x,y: single;
begin
x:=0.00000001;
y := sqrt(x*x + 1) - 1;
writeln('W pierwszym przypadku: y = ', y);
x:=0.00000001;
y := x*x / (sqrt(x*x + 1) + 1);
writeln('W drugim przypadku : y = ', y);
readln;
end.
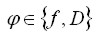 (należy
do klasy zadań
(należy
do klasy zadań  ) jeżeli
) jeżeli 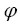 jest alg. obliczenia
wyniku y=f(x) dla
dowolnych danych
jest alg. obliczenia
wyniku y=f(x) dla
dowolnych danych 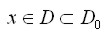
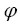 nazywamy
numerycznie poprawnym w klasie zadań
nazywamy
numerycznie poprawnym w klasie zadań 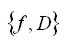 jeżeli istnieją
stałe Cx,
Cy takie, że
jeżeli istnieją
stałe Cx,
Cy takie, że 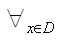 i dostatecznie
silnej arytmetyki instnieje
i dostatecznie
silnej arytmetyki instnieje 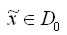 takie, że
takie, że 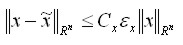
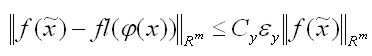
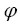 w klasie zadań
w klasie zadań 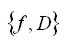
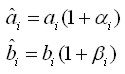 , gdzie
, gdzie 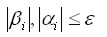
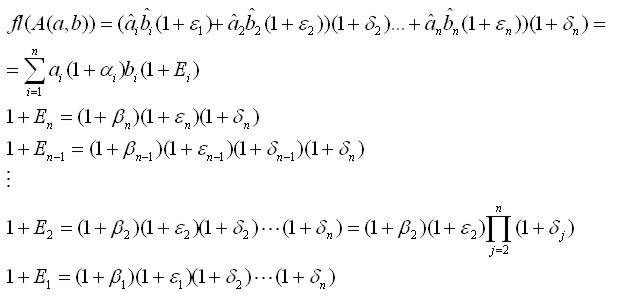
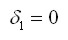 to otrzymujemy:
to otrzymujemy: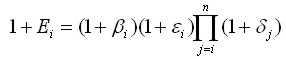
 , gdzie
, gdzie 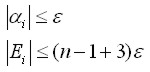
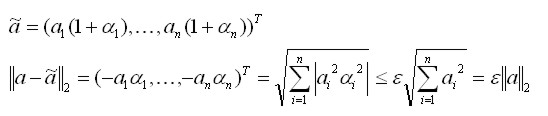
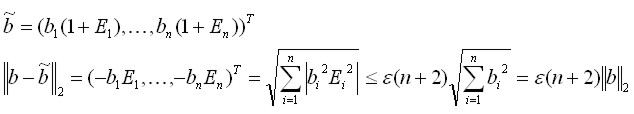
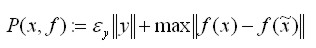 nazywamy
optymalnym poziomem błędu rozwiązania f(x) w arytmetyce fl.
nazywamy
optymalnym poziomem błędu rozwiązania f(x) w arytmetyce fl.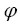 nazywamy numerycznie
stabilnym w
klasie zadań
nazywamy numerycznie
stabilnym w
klasie zadań 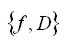 jeżeli istnieje
stałą C taka, że
jeżeli istnieje
stałą C taka, że 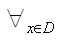 i dla dostatecznie
silnej arytmetyki
i dla dostatecznie
silnej arytmetyki 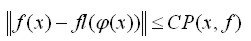
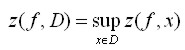 , gdzie z(f,x)
oznacza minimalną liczbę działań potrzebnych do obliczenia f(x),
nazywamy złożonością obliczeniową.
, gdzie z(f,x)
oznacza minimalną liczbę działań potrzebnych do obliczenia f(x),
nazywamy złożonością obliczeniową.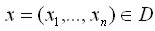 , dla których
zmiana dowolnej ze składowych x powoduje zmianę wyniku.
, dla których
zmiana dowolnej ze składowych x powoduje zmianę wyniku.