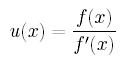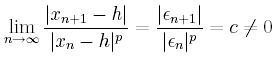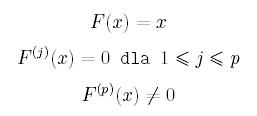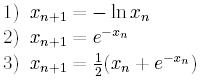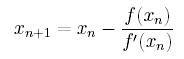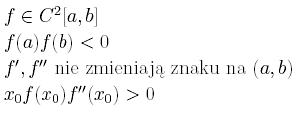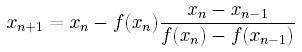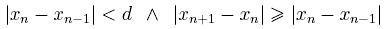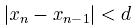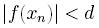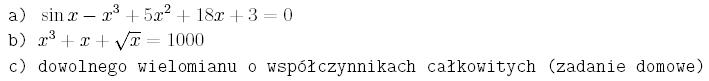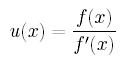Metody numeryczne 1
(MEN331) - Ćwiczenia 8
Kalendarium,
Zasady, Ćw1,
Ćw2, Ćw3, Ćw4, Ćw5, Ćw6, Ćw7, Ćw8, Ćw9, Ćw10, Ćw11,
Ćw12, Ćw13
Prowadzący: Rafał Witkowski
Temat: Rozwiązywanie równań
metodami iteracyjnymi: metoda bisekcji, metoda stycznych (metoda
Newtona), metoda siecznych, kryteria stopu
Rząd metody iteracyjnej
Definicja
Mówimy, że w punkcie h metoda
jest rzędu p, jeśli istnieje
liczba rzeczywista p>=1 taka, że
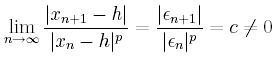
liczbę c nazywamy stałą
asymtotyczną błędu.
Twierdzenie
Rząd każdej metody iteracyjnej jednokrokowej jest liczbą naturalną.
Funkcja iteracyjna F(x) ma rząd p wtedy
i tylko wtedy, gdy
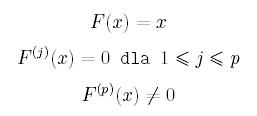
Zadanie 1
Aby rozwiązać równanie x+lnx = 0 można wybrać jeden z następujących
wzorów:
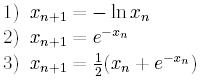
a) Który z tych wzorów można użyć?
b) Który z tych wzorów będzie najlepszy do użycia?
Metoda bisekcji
Metoda ta polega na wpierw znalezieniu wpierw dwóch punktów a i b dla których f(a)*f(b) < 0.
Następnie należy wybrać środek tego przedziału i zobaczyć jaki on ma
znak. Następnym przedziałem, który będziemiy rozpatrywać będzie ten,
który będzie w dalszym ciągu spełniał nasz warunek początkowy, czyli
jego znaki będą od siebie różne. Jeśli w środku przedziału wartość
będzie równa 0, to oczywiście znaleźliśmy miejsce zerowe i nie musimy
nic dalej robić.
Metoda ta po n krokach daje nam dokładność 2^n, czyli 1 bit rozwinięcia
dziesiętnego na każdy krok. Jest to więc rozwiązanie takie sobie...
Metoda stycznych
Jest to metoda, która działa poprzez poprowadzenie do wykresu funkcji
stycznej w punkcie x(n) i
przyjęcia za x(n+1) punktu
przecięcia tej stycznej z osią OX.
Wzór na tą metodę jest następujący:
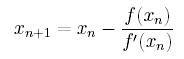
Warunki dostateczne zbieżności
Do działania metody stycznej wystarczy spełnienie następujących
warunków (wszystkich):
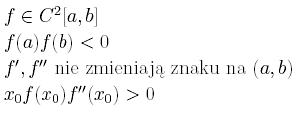
Metoda siecznych
Jest to metoda dwukrokowa, co oznacza, że aby z niej skorzystać trzeba
do obliczania kolejnego przybliżenia używać dwóch poprzednich
przybliżeń. Działa ona w taki sposób, że przez dwa poprzenie punkty (x,
f(x)) przepuszcza się prostą, które one wyznaczają, a kolejne
przybliżenie jest przecięciem się tej prostej z osią OX.
Wzór na tą metodę jest następujący:
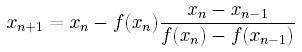
Kryteria stopu
Problem zatrzymywania iteracji, które muszą wykonać pewną liczbę
kroków, żeby dostać zadowalającą nas dokładność, jest problemem bardzo
złożonym. Na wykładzie zostało dokładnie omówione dlaczego często nie
możemy zrobić tego dobrze wprost.
W warunkach rzeczywistych możemy zakończyć iteracje i uznać, że
osiągnęliśmy już zadowalające nas przybliżenie pierwiastka danego
równania jeśli jednocześnie spełnione są następujące warunki:
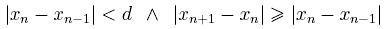
gdzie d jest jest pewną
graniczną tolerancją używaną tylko po to, aby zapobiec przedwczesnemu
zatrzymaniu.
Grube stopowanie
Do stopowania obliczeń możemy też stosować tzw. grube stopowanie, które
nie jest tak dobre jak dokładne kryterium stopu podane wcześniej,
niemniej często ze względu na złożoność obliczeniową także stosowane.
Są dwa rodzaje owego grubego stopowania.
1) Stopujemy iteracje, jeśli tylko 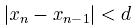
2) Stopujemy iteracje, jeśli zadzodzi warunek 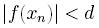
Zadanie 2
Napisz program, który obliczy przy pomocy metody bisekcji i siecznych
pierwiastek równania:
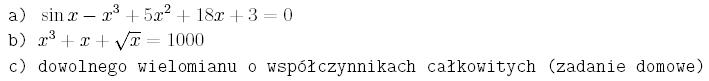
Pierwiastki wielokrotne
Omówionych wcześniej metod iteracyjnych oczywiście nie da się stosować
w przypadku, gdy mamy do czynienia z pierwiastkami wielokrotnymi.
W takim przypadku dobry rozwiązaniem będzie to, jeśli zamienimy funkcję
f, które pierwiastka szukamy i zastąpimy ją przez nową funkcję postaci: