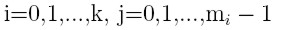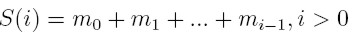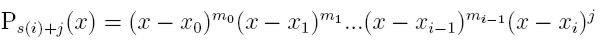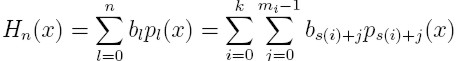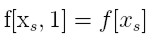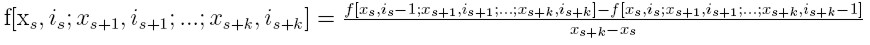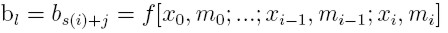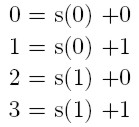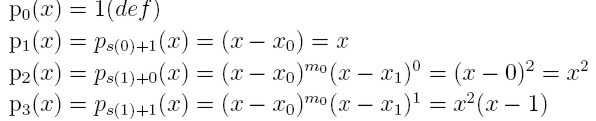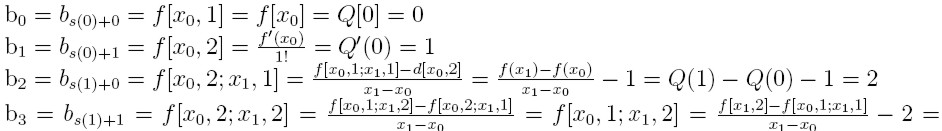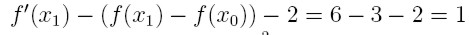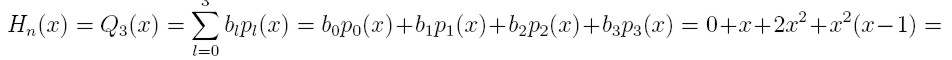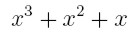Przypadek węzłów wielokrotnych
Przy podawanych poniżej założeń o regularności funkcji
f, jej ilorazy
różnicowe oparte na wielokrotnych węzłach określa się następująco
(według odpowiedniego twierdzenia):
- dla węzłów wielokrotnych o krotnościach i
Otrzymujemy współczynniki b:
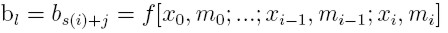
Przykład 5
Zajdź wielomian 3 topnia Q(x) taki, że
Q(0) = 0, Q'(0) = 1
Q(1) = 3, Q'(1) = 6
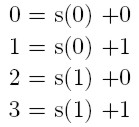
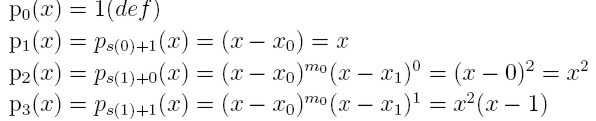
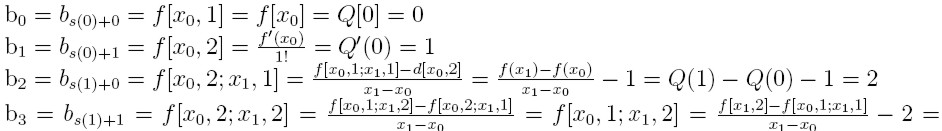
Zadanie 4
Znajdź wielomian interpolacyjny Hermite'a, wiedząc o funkcji, że:
a) f(2)=1, f'(2) = 2, f''(2) = 0, f(3) = 1,
f'(3) = 2;
b) f(2) =1, f(4) = 1, f'(4) = 1,
f''(4) = 1
Reszta interpolacyjna
Resztę interpolacyjną wielomianu w postaci Hermite'a oblicza się
zupełnie tak samo jak to było przy postaci Lagrange'a. Należy jedynie
zwrócić uwagę na to, że oczywiście wielomian p(x), który jest we wzorze
na obliczanie reszty wygląda nieco inaczej, a poza tym zupełnie nic sie
nie zmienia.
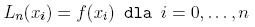
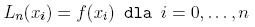
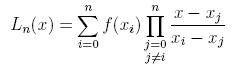
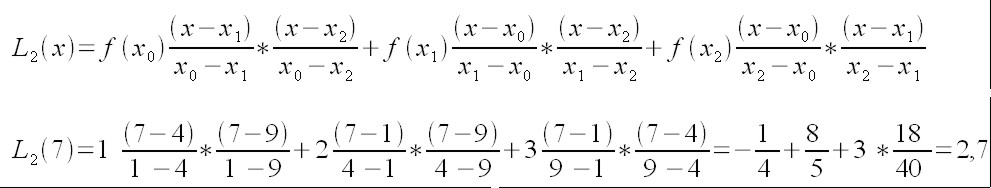
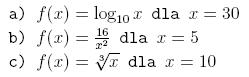
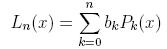 ,
gdzie
,
gdzie 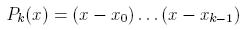
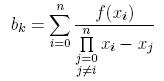
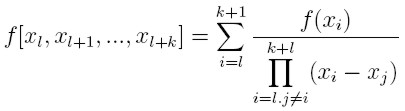
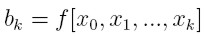
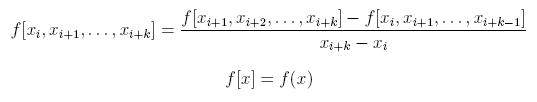
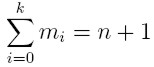
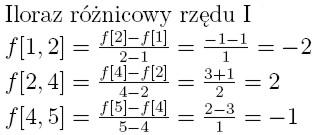
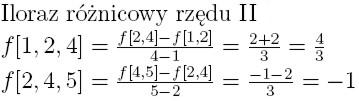
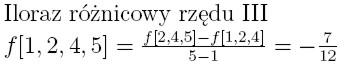
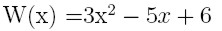 oraz punktów:
oraz punktów: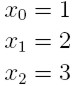
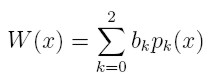
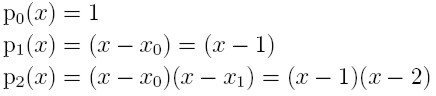
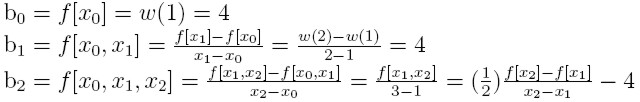
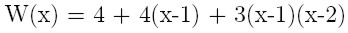
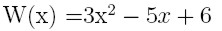 dla punktów 0, 1,
3.
dla punktów 0, 1,
3.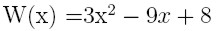 dla punktów 3
dowolnie wybranych punktów.
dla punktów 3
dowolnie wybranych punktów.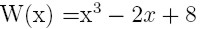 dla 4 dowolnie
wybranych punktów.
dla 4 dowolnie
wybranych punktów. 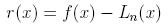
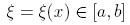 zależny od punktu x dla którego:
zależny od punktu x dla którego: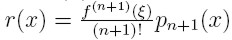
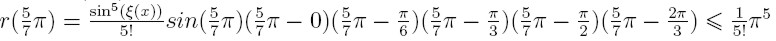
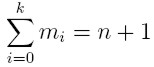
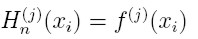 dla
dla