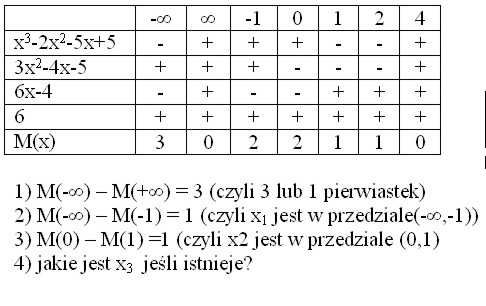
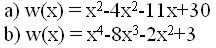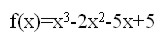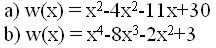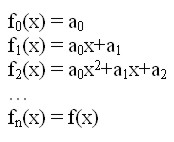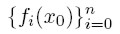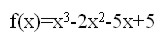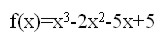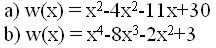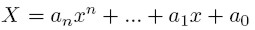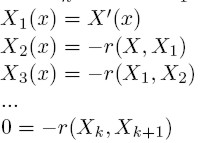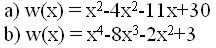Następnie oznaczamy przez L(x0) liczbę zmian znaku w ciągu
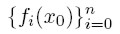
Twierdzenie Laguerre'a
Jeżeli f(x)jest wielomianem stopnia n olreślonym na przedziale (a,b) i
f(a)f(b)<>0 to liczba zer wielomianu f(x) w tym przedziale jest
równa L(a) - L(b) lub jest od tej liczby mniejsza o liczbę parzystą
Przykład 2
Wyznaczyć ilość pierwiastków równania:
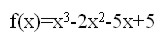
Rozwiązanie: