Metody numeryczne 1 (MEN331) - Ćwiczenia 13

Kalendarium, Zasady, Ćw1, Ćw2, Ćw3, Ćw4, Ćw5, Ćw6, Ćw7, Ćw8, Ćw9, Ćw10, Ćw11, Ćw12, Ćw13
Prowadzący: Rafał Witkowski
Temat: Algorytm Bairstowa, powtórki

Metoda Bairstowa

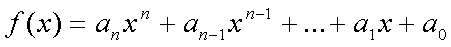
Metoda Bairstowa służy do znajdowania przybliżonych wartości pierwiastków zespolonych wielomianu:

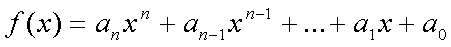
o współczynnikach rzeczywistych (ak należą do rzeczywistych, k=0,1,2,...,n)

Metoda Bairstowa unika arytmetyki zespolonej. Opiera się na twierdzeniu:

 Twierdzenie

Zera rzeczywistego wielomianu kwadratowego x2-px-r są zerami danego wielomianu rzeczywistego f(x) wtedy i tylko wtedy, gdy wielomian f(x) można
podzielić bez reszty przez x2-px-r.

 

Zatem gdy znajdziemy dzielniki kwadratowe wielomianu f(x) będziemy mieli jego zera. Taki rozkład wielomianu na dzielniki kwadratowe (z ewentualnym jednym liniowym czynnikiem rzeczywistym, gdy stopień wielomianu n jest nieparzysty) istnieje, gdyż każdemu zespolonemu zeru wielomianu f(x) odpowiada zero sprzężone, a dzielnik ma współczynniki rzeczywiste. Co łatwo mozna pokazać:
niech ,wtedy = x2-2ax+a2+b.
Szukamy takich p,r aby wielomian kwadratowy x2-px-r dzielił f(x) bez reszty.
Niech m(x) = m(x;p,r) = x2-px-r będzie dowolnym trójmianem kwadratowym o współczynnikach rzeczywistych. Dzieląc wielomian f(x) otrzymamy iloraz Q i  resztę, tzn:
f(x) = m(x;p,r) * Q(x;p,r) + q1(p,r)x + q0(p,r).

Stąd widać, że trójmian m*(x;p,r) jest dzielnikiem wielomianu f(x) wtedy i tylko wtedy, gdy q1(p*,r*) = q0(p*,r*) = 0

Reasumując, jeżeli chcemy znaleźć takie p*, r*, aby wielomian kwadratowy x2-p*x-r* dzielił f(x) bez reszty, musimy rozwiązać układ dwóch równań nieliniowych o dwóch niewiadomych:

Metoda Bairstowa polega na zastosowaniu dwuwymiarowej metody Newtona do tego układu. Dla danego przybliżenia początkowego [p0,r0] wektora [p*,r*]  konstrujemy ciąg {[pk,rk]} określony zależnościami:

 
       

Po znalezieniu takich p*, r* dzielimy wielomian f(x) przez m* i jeżeli stopień f(x)=f(x)/m* jest >= 2 znów szukamy kolejnego dzielnika m*.
Oczywiście znalezione p, r są przybliżeniami p*, r* na tyle dobrymi, że q1(p,r) <eps i q0(p,r) <eps dla zadanej wartości eps (która jest odpowiednio mała)

Problemy 

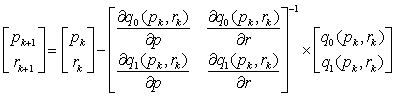
Wartości 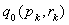, 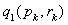można otrzymać za pomocą następujących wzorów rekurencyjnych:

 

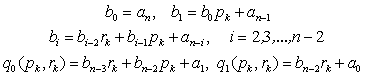
Pochodne cząstkowe wyznacza się na podstawie wzorów:


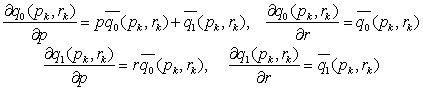
gdzie wartości 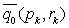, 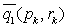mogą być obliczone na podstawie podobnych wzorów rekurencyjnych, a mianowicie:

Zadanie 1

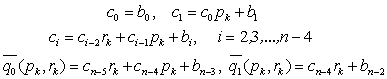
Przy pomocy algorytmu Bairstowa oblicz pierwiastki wielomianu:


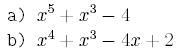
Do obliczenia każdego pierwiastka wykonaj co najmniej dwa jego przybliżenia. Podaj wynik, czyli wszystkie (przybliżone) pierwiastki tego równania.

Zadanie domowe

Nauczyć się porządnie na kolowkium, podczas którego mogą pojawić się pytania o:
- Obliczanie rozwiązań równania za pomocą interpolacji odwrotnej
- Metoda iteracyjna obliczania pierwiastków liczb naturalnych
- Konstrukcja wzorów iteracyjnych
- Obliczanie rzędu i stałej asymptotycznej błędu metody iteracyjnej
- Metoda bisekcji, stycznych i siecznych
- Metoda Fouriera
- Metoda Laguerre'a
- Reguła Kartezjusza
- Algorytm Sturma
- Kwadratury interpolacyjne
- Kwadratury N-C
- Metoda Jacobi'ego
- Metoda Gaussa-Seidla
- Algorytm Bairstowa