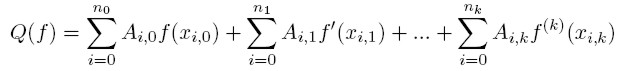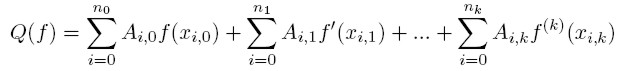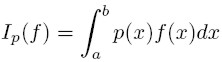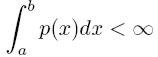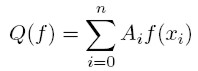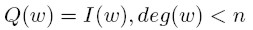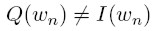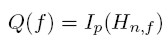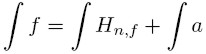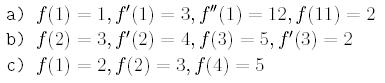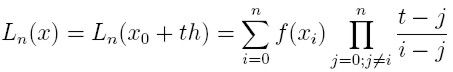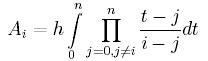Metody numeryczne 1 (MEN331) - Ćwiczenia 11

Kalendarium, Zasady, Ćw1, Ćw2, Ćw3, Ćw4, Ćw5, Ćw6, Ćw7, Ćw8, Ćw9, Ćw10, Ćw11, Ćw12, Ćw13
Prowadzący: Rafał Witkowski
Temat: Całkowanie numeryczne: kwadratury interpolacyjne: trapezu, Newtona-Cotesa

Idea całkowania numerycznego

Czasami wyznaczenie funkcji pierwotnej i obliczenie danej całki może być bardzo trudne lub czasem wręcz niemożliwe. Ten problem można spróbować rozwiązać za pomocą aproksymacji numerycznej danej całki.
W praktyce dysponujemy często procedurą obliczania wartośći podcałkowej f(x) i ewnetualnie procedurami obliczania pochodnych funkcji f(x), f'(x), f''(x), f'''(x) itd. lub też często dysponujemy też tablicą funkcji podcałkowej. Naturalne jest więc przybliżanie całki funkcjonałami Q(f):



Takie funkcjonały nazywamy kwadrawturami liniowymi, a współczynniki ai,j nazywamy współczynnikami kwadratur, a punkty xi,j węzłami.

Rozaważać będziemy też ogólniejszą postać przybliżonych całek:


gdzie funkcja wagowa p(x) jest nieujemna na [a,b], zeruje się w nim w skończonej liczbie punktów i jest całkowalna,


Najczęściej stosowanymi są kwadratury korzystające z wartości funkcji f tj. kwadratury w postaci:


Posiadają one 2n+3 parametrów.

Wybór konkretnych parametrów może być podyktowany różnymi względami. Możemy np. rządać minimalizacji reszty kwadratury R(f)

R(f) = I(f) - Q(f)
w ustalonej klasie funkcji.

Definicja - rząd kwadratury

Mówimy, że kwadratura Q(f) ma rząd n jeżeli jest dokładna dla wszystkich wielomianów stopnia mniejszego niż n tzn.


Oraz instnieje wielomian stopnia n taki, że

Definicja kwadratury interpolacyjnej

Przez kwadraturę interpolacyjną rozumiemy kwadraturę otrzymaną przez scałkowanie wielomianu interpolacyjnego Hermite'a Hn,f funkcji podcałkowej tj



Dla otrzymania reszty kwadrtury R(f) = I(f) - Q(f) należy korzystać z przedstawienia reszty interpolacyjnej.

Zadanie 1

Znając wartości funkcji w punkcie i niektórych jego pochodnych, oblicz przybliżoną całkę z tej funkcji:


Kwadratury Newtona-Cotesa (N-C)

Definicja

Kwadraturami N-C nazywamy kwadratury otrzymane z całkowania wielomianu interpolacyjnego Lagrange'a funkcji f opartego na równoodległych węzłach xi
czyli
x0 = a,
xi = x0 + i*h, gdzie h=(b-a)/n  
xn=b
 Dla węzłów równoodległych wielomian Lagrange'a przyjmuje postać:

Otrzymujemy zależność:

Zadanie 2

Wyprowadź kwadrature Newtona-Cotesa dla:
a) n=1 (wzór trapezów)
b) n=2 (wzór Simpsona)

Zadanie 3

Oblicz całkę z sin x na przedziale od 0 do pi/2 za pomocą:

a) wzoru trapezów
b) wzoru simpsona