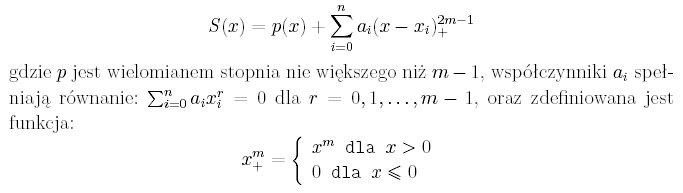Metody numeryczne 1
(MEN331) - Ćwiczenia 6
Kalendarium,
Zasady, Ćw1,
Ćw2, Ćw3, Ćw4, Ćw5, Ćw6, Ćw7, Ćw8, Ćw9, Ćw10, Ćw11,
Ćw12, Ćw13
Prowadzący: Rafał Witkowski
Temat: Interpolacje
wielomianowe węzłów równoodległych, interpolacje funkcjami sklejanymi
Interpolacja dla węzłów równoodległych
Często węzły interpolacyje są równo odległe tzn. oddalone od siebie o
tą samą wartość (x(i+1) - x(i) = h)
h nazywamy krokiem (odległość 2-ch sąsiednich węzłów)
Wzór Lagrange'a przyjmuje wtedy postać:
Aby określić postać Newtona tego wielomianu Lagrange'a zdefiniujmy
wpierw różnicę progresywną
rzędu k funkcji f :
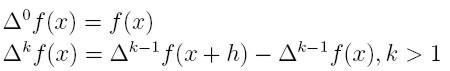
Dla węzłów równoodległych uzyskujemy następującą zależność:
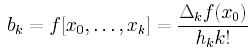
Prawdziwe są także następujące wzory:
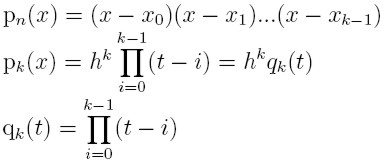
A zatem postać Newtona wielomianu interpolacyjnego Lagrange'a dla
węzłów równoodległych jest równa:
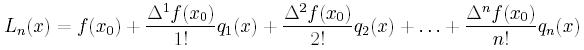
Zadanie 1
Wyznacz wielomian interpolacyjny Lagrange'a przy węzłach
równoodległych, wiedząc, że:
a) f(1) = 2, f(2) = 2, f(3) = 1, f(4) = 5
b) f(-1) = 3, f(1) = 2, f(3) = 4, f(5) = 2
Interpolacja funkcjami sklejanymi (splajnami)
Znając wartości funkcji w kilku punktach możemy ją także interpolować
przy pomocy naturalnych funkcji sklejanych S(x). Każdą taką funkcję
określoną na punktach 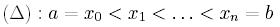 da się
jednoznacznie wyznaczyć z wzorów:
da się
jednoznacznie wyznaczyć z wzorów:
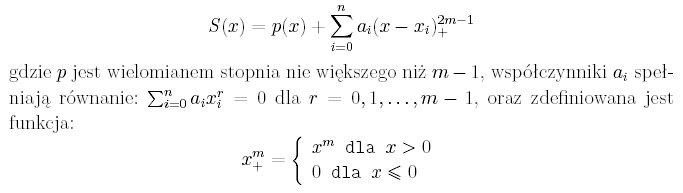
Podstawiając wszystkie dane otrzymamy m+n równań liniowych z m+n
niewiadomymi, które po rozwiązaniu da nam wszystkie potrzebne
wpółczynniki, które właśnie jednoznacznie wyznaczają wielomian S(x).
Zadanie 2
Wyznacz wielomian interpolacyjny przy pomocy funkcji sklejanych
wiedząc, że:
a) f(1) = 2, f(2) = 2, f(3) = 1, f(4) = 5
b) f(0) = 3, f(1) = 2, f(3) = 4, f(5) = 2
Wyznacz wartości tych wielomianów w punkcie f(2,5)
Zadanie 3 (zadanie domowe)
Nauczyć się porządnie na kolokwium.
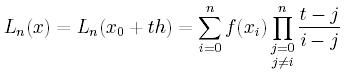
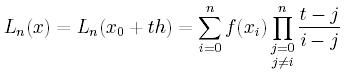
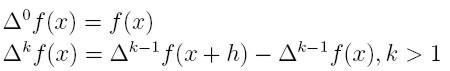
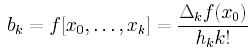
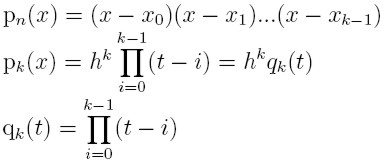
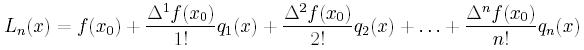
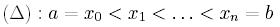 da się
jednoznacznie wyznaczyć z wzorów:
da się
jednoznacznie wyznaczyć z wzorów: