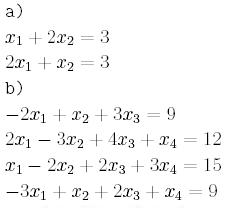Metody numeryczne 1
(MEN331) - Ćwiczenia 12
Kalendarium,
Zasady, Ćw1,
Ćw2, Ćw3, Ćw4, Ćw5, Ćw6, Ćw7, Ćw8, Ćw9, Ćw10, Ćw11,
Ćw12, Ćw13
Prowadzący: Rafał Witkowski
Temat: Metody
rozwiązywania równań liniowych.
Na ten czas będziemy zajmować sie metodami rozwiązywania równań
liniowych, czyli równań postaci Ax =
b, gdzie b jest danym
wektorem, A macierzą
przejścia, a x szukanym
wektorem.
Jeśli przyjmiemy, że G jest pewną nieosobliwą macierzą o odpowiednich
wymiarach możemy zrobić następujące przekształcenia:
Czyli po dokonaniu odpowiednich podstawień, można uzyskać metodę
iteracyjną rozwiązywania układów równań liniowych:
Aby ta metoda iteracyjna działała w miarę sprawnie powinny być
spełnione następujące warunki co do macierzy G:
- macierz G powinna się łatwo obracać
- wartości własne macierzy B powinny być możliwe małe co do modułu
Warunki zbieżności
Aby powyższa metoda była zbieżna, wystarczy, aby dowolna norma macierzy
B zgodna z jakąkolowiek norm wektorowych była mniejsza od 1.
Normą taką mogą być np:
Promień spektralny macierzy
Promieniem spektralnym macierzy A nazywamy wartość:
UWAGA! promień spektralny jest również dobrym operatorem do sprawdzania
zbieżności metody iteracyjnej rozwiązywania równań liniowych. Jego
wartość mnusi być mniejsza od 1, aby metoda była zbieżna.
Wybór metody
W przypadku, gdy do wyboru mamy więcej zbieżnych metod rozwiązywania
układu równań liniowych, najlepiej jest wybrać tą z najmniejszym
promieniem spektralnym.
Metoda Jacobiego
Będziemy rozwiązywać układ równań postaci Ax = b.
Przedstawmy daną macierz A w
postaci A = L + D + U, gdzie L jest
macierzą, która na przekątnej i nad nią ma same zera, a pod nią
wartości takie same jak A, U jest analogiczną macierzą, która
na przekątnej i pod nią ma same 0, a nad nią te same wartości co A, natomiast macierz D jest macierzą, która na
przekątnej jest taka sama jak A,
a poza nią jest wyzerowana.
Jako macierz G wybieramy w
tej metodzie macierz D. Wtedy:
Macierz 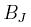 nazywamy macierzą
Jacobi'ego.
nazywamy macierzą
Jacobi'ego.
Zadanie 1
Wyznacz dokładne wzory na przybliżanie kolejnych współrzędnych wektora
x. (czyli wzór ogólny na xi).
Zadanie 2
Oblicz przy pomocy metody Jacobi'ego układ równań:
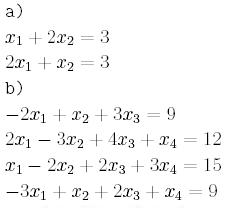
Wyznacz macierz Jacobi'ego i przeprowadż dwa kroki przybliżające
rozwiązanie zaczynąjąc od wektora początkowego [2,2,2,2]
Metoda Gaussa-Seidla
W tej metodzie jako macierz G
wybierzmy macierz postaci G = L + D,
gdzie macierze L i D są zdefiniowane tak samo jak
poprzednio przy metodzie Jacobi'ego.
UWAGA! trzeba uważać, żeby taka macierz była odwracalna. Będzie tak
tylko wtedy, jeśli wszystkie elementy na przekątnej macierzy A są odwracalne.
Jeśli tak wybierzemy macierz G
wtedy mamy:
Macierz 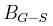 nazywamy macierzą
Gaussa-Seidla.
nazywamy macierzą
Gaussa-Seidla.
Zadanie 3
Wyznacz dokładne wzory na przybliżanie kolejnych współrzędnych wektora
x. (czyli wzór ogólny na xi).
Zadanie 4
Oblicz przy pomocy metody Gaussa-Seidla układ równań:
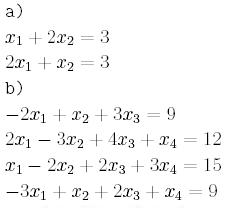
Wyznacz macierz Gaussa-Seidla i przeprowadż dwa kroki przybliżające
rozwiązanie zaczynąjąc od wektora początkowego [2,2,2,2]
Zadanie 5
Która metoda jest lepsza dla rozwiązywanych przykładów?
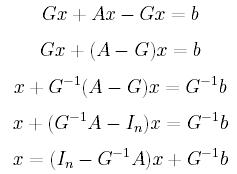
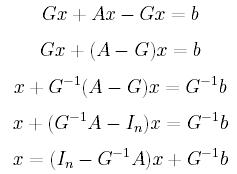
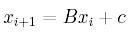
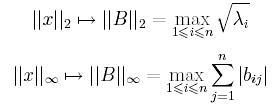
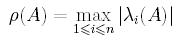
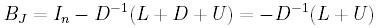
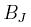 nazywamy macierzą
Jacobi'ego.
nazywamy macierzą
Jacobi'ego.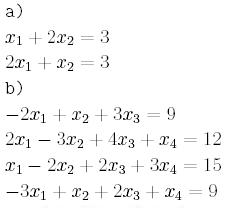
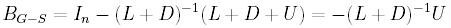
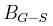 nazywamy macierzą
Gaussa-Seidla.
nazywamy macierzą
Gaussa-Seidla.