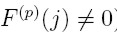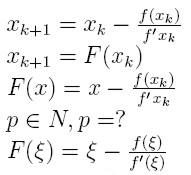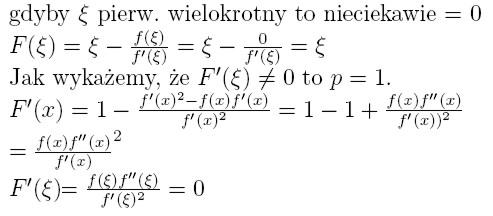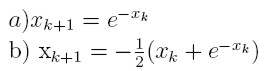Metody numeryczne 1
(MEN331) - Ćwiczenia 7
Kalendarium,
Zasady, Ćw1,
Ćw2, Ćw3, Ćw4, Ćw5, Ćw6, Ćw7, Ćw8, Ćw9, Ćw10, Ćw11,
Ćw12, Ćw13
Prowadzący: Rafał Witkowski
Temat: Interpolacja odwortna,
metody iteracyjne
rozwiązywania równań liniowych
Interpolacja odwrotna
Interpolacja odrotna jest jedną z podstawowych metod rozwiązywania
następującego zagadnienia:
Niech y=f(x) będzie funkcją, której 0 (zero) bądź zera chcemy znaleźć.
Załóżmy, że funkcja ta jest stablicowana na pewnym zbiorze argumentów
x
|
y=f(x)
|
x0
|
y0=f(x0)
|
x1
|
y1=f(x1)
|
...
|
... |
xn
|
yn=f(xn)
|
Załóżmy, żę funkcja spełnia założenia twierdzenia o funkcji
odwrotnej. Możemy więc napisać x= g(y), gdzie g jest funkcją odwrotną
do funkcji f. Dlatego obliczenie wartośći funkcji g w punkcie 0 jest
równoważne wyznaczaniu zera funkcji f.
f(x)=y
|
g(y)=x
|
y0
|
x0
|
y1
|
x1
|
...
|
... |
yn
|
xn
|
Niech teraz wykorzystując język interpolacji liczby y0=f(x0),
.. yn=f(xn)
będą węzłami zmiennej niezależnej yj, a x0, ... , xn - wartościami
funkcji g w tych węzłach. Aproksymację g(y) wielomianem interpolacyjnym
zbudowanym na bazie powyższej tablicy i interpolując w punkcie y=0
otrzymujemy szukane przybliżenie zera funkcji f.
Błąd interpolacji odwrotnej ma postać:
Przykład 1
Przy pomocy interpolacji odwrotnej wyznaczymy pierwiastek z dwóch
metodami analogicznymi jak na poprzednich ćwiczeniach.
Zadanie 1
Oblicz za pomocą interpolacji odwrotnej rozwiązanie równania:
a) log x = 2,5
b) arcsin x = 0,9
c) 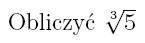
Metoda iteracyjna rozwiązywania równań liniowych
Jednym z najczęściej pojawiających się w różnych kontekstach
pomysłów obliczeniowych jest iteracja czyli kolejne powtarzanie (w celu
przybliżenia wyniku). Ogólnie iteracja oznacza powtarzanie pewnej
czynności lub procesu np. wielokrotne stosowanie procesu numerycznego,
który może być bardzo złożony, po to by stopniowo ulepszać wcześniejsze
wyniki.
Załóżmy, że x=F(x) , gdzie F - różniczkowalna funkcja, której wartości
możemy obliczyć dla argumentu z zadanej dziedziny. Stosując metodę
iteracji, zaczynamy od przybliżenia początkowego x0 i konstruujemy ciąg
x0, x1=F(x0),
x2=F(x1),
... itd. Każde obliczenie postaci xi+1 =
F(xi) nazywamy iteracją.
Jeżeli ciąg xi jest zbieżny do wartości granicznej alfa to wówczas mamy:
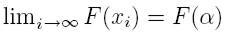
i punkt alfa jest rozwiązaniem
równania x = F(x)
Gdy i rośnie spodziewamy
się,
że kolejne wartośći xi są coraz lepszymi przybliżeniamy szukanego
pierwiastka. W związku z szerokimi zastosowaniami ideii iteracji rodzą
się naturalne pytania dotyczące własności ciągu Fi.
1) Czy ciąg jest zbieżny?
2) Jeżeli tak, to jak szybko jest zbieżny?
Rozwiązywanie układów równań liniowych i nieliniowych
Bardzo często iterację stosuje się do rozwiązywania ukł. równań
liniowych i nieliniowych. Wtedy xi jest ciągiem wektorów, a F jest
funkcją o wartościach wektorowych
Wzór wynikający z twierdzenia o wartości średniej:
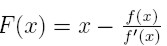
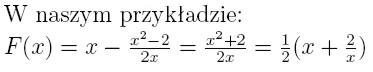
Zadanie 2
Za pomocą iteracji oblicz:
a) pierwiastek z 3
b) pierwiastek z 5
Szybka metoda obliczania pierwiastków kwadratowych
Przykład 2
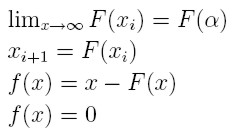

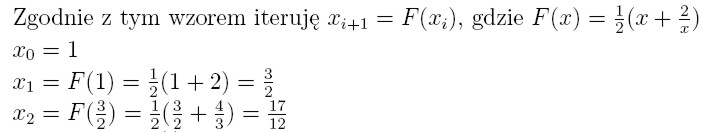
czyli uzyskaliśmy wynik że pierwiastek z 2 wynosi w przybliżeniu
1,416666 co wydaje się być nawet bardzo dobrym przybliżeniem biorąc pod
uwagę ilość iteracji.
Uwaga: Powyższy sposób
obliczania pierwiastków kwadratowych stosuje się w kalkulatorach i
komputerach.
Zadanie 3
Obliczyć pierwiastek równania kwadratowego 
Zadanie 4 (zadanie domowe)
Napisz program umożliwiający obliczanie pierwiastków drugiego stopnia z
dowolnej liczby.
Niech program oblicza ten pierwiastek z dokładnością do 3 miejsc po
przecinku.
UWAGA! Do obliczania oczywiście nie wolno używać procedury sqrt()!
Konstrukcja wzorów iteracyjnych
Konstrukcja wprost z rozwiązywanego problemu:
Bardzo często funkcje F dane są wraz ze sformułowanym zagadnieniem np.
jeżeli mamy rozwiązać równianie:
x - cos x = 0 (lub np. ln x + x = 0)
Popatrzmy ze wzoru x= F(x)
x= cos x
x = F(x)
więc
F(x) = cos x
xi+1 = F(xi)
|F'(x)| <1 - czyli generuje się zbieżny ciąg
wartości, przybliżamy wynik
Przykład 3
Obliczyć pierwiastek równania: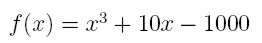
Patrząc na równanie widać że pierwiastek ten jest z przedziału [9,10].
1) Pomysł:
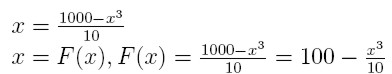
Jednak zobaczmy czy |F'(x)| spełnia założenie |F'(x)|<1 ? Okazuje
się, że: 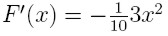 , czyli nie jest
spełnione założenie zbieżności i trzeba wymyśleć inny sposób:
, czyli nie jest
spełnione założenie zbieżności i trzeba wymyśleć inny sposób:
2) Pomysł:
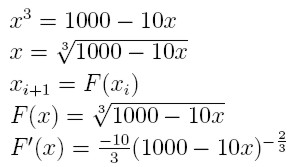
Czyli teraz jest dobrze!!!
Zadanie 5
Oblicz wprost rozwiązanie równania:
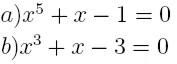
Rozwinięcie w szereg Taylora:
Funkcje iteracyjne F możemy systematycznie otrzymać w następujący
sposób:
Jeżeli Z jest
zerem funkcji f: R->R, funkcja f jest w otoczeniu U(Z) punktu Z
dostatecznie wiele razy różniczkowalna, to z rozwinięcia funkcji f wg.
wzoru Taylora wokół punktu xo otrzymujemy:
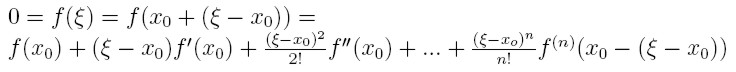
Zaniedbując wyrazy wyższego rzędu otrzymujemy wzory, które dla danego
x0 muszą spełniać przybliżenia szukanego zera:
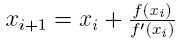
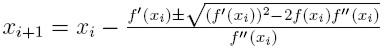
Otrzymane wzory nazywamy wzorami Newtona
- Robstona. Ogólnie mówimy o metodzie v stopnia jeżeli rozwinięcie
funkcji f w szereg Taylora, kończymy na wyrazie (xi - x_0)^v.
Metody iteracyjne rozwiązywania równania f(x)=x0 korzystające z
iteracji odwrotnej
Niech g(y) będzie funkcją odwrotną do funkcji f(x). Przy danych
punktach
j( j=0,1,...,n) możemy funkcję g(y) aproksymować za pomocą wielomianu
interpolacyjnego Lagrange'a
(*) 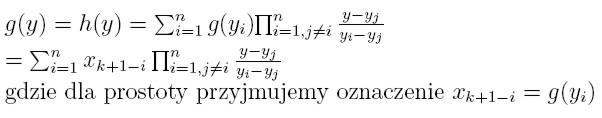
Chcemy znależć taką wartość 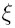 zmiennej x, dla
której y=f(
zmiennej x, dla
której y=f(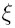 )=0. Ponieważ
)=0. Ponieważ 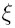 =g(0), więc ze wzoru
(*) otrzymujemy
=g(0), więc ze wzoru
(*) otrzymujemy
(**) 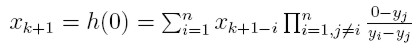
Stąd na mocy postaci reszty interpolacyjnej mamy (***)
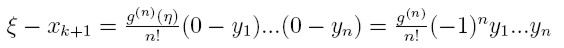
Wzór (**) określa metodę iteracyjną obliczania pierwiastka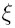 równania f(x) = 0
(Jeżeli proces iteracyjny jest zbieżny). Metoda ta polega na tym, że z
punktów
równania f(x) = 0
(Jeżeli proces iteracyjny jest zbieżny). Metoda ta polega na tym, że z
punktów
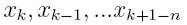 obliczamy
obliczamy 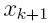 , a następnie
zastępując jeden z punktów
, a następnie
zastępując jeden z punktów 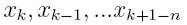 punktem
punktem 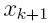 obliczamy
obliczamy 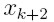 itd.
itd.
Obliczanie rzędu każdej, jednokrokowej metody iteracyjnej
Twierdzienie. Rząd każdej,
jednokrokowej metody iteracyjnej postaci:  jest liczbą
naturalną. Dokładnie dunkcja iteracyjna F ma rząd p <=>
jest liczbą
naturalną. Dokładnie dunkcja iteracyjna F ma rząd p <=> 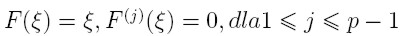 i
i 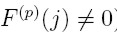
Przykład 4
Zbadać rząd metody Newtona:
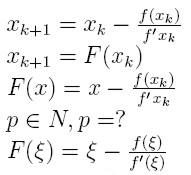
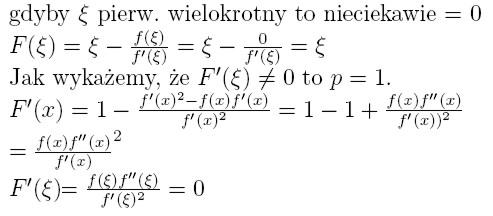
stąd rząd metody Newtona = 2 (dla szczególnych funkcji f rząd metody
Newtona może być wyższy)
Wybór metody iteracyjnej
Przekształcenia równania f(x) = 0 na równanie postaci x = F(x) można
dokonywać na wiele sposobów. Wśród zbieżnych metod iteracyjnych
wybieramy tę metodę, której funkcja iteracyjna ma najmniejszy moduł
pochodnej.
Zadanie 6
Dane są następujące dwie metody iteracyjne rozwiązujące równanie x+ ln
x = 0
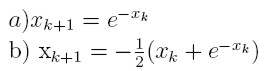
której metody należy użyc, aby wyliczyć jej wartość w punkcie 2?
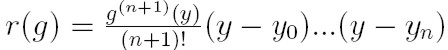
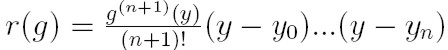
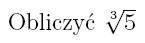
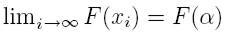
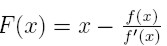
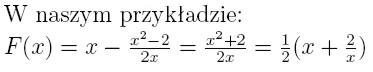
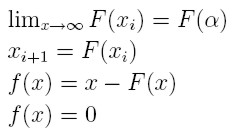

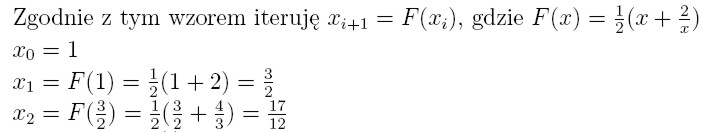

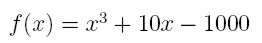
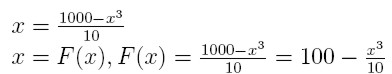
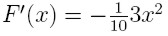 , czyli nie jest
spełnione założenie zbieżności i trzeba wymyśleć inny sposób:
, czyli nie jest
spełnione założenie zbieżności i trzeba wymyśleć inny sposób: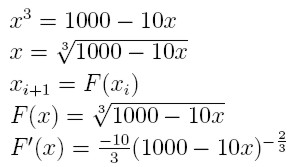
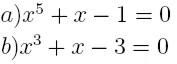
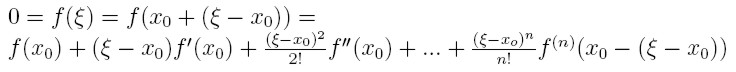
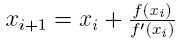
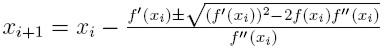
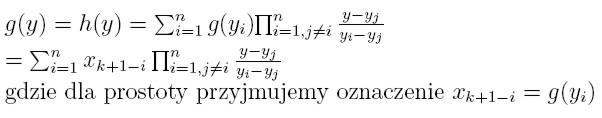
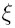 zmiennej x, dla
której y=f(
zmiennej x, dla
której y=f(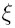 )=0. Ponieważ
)=0. Ponieważ 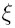 =g(0), więc ze wzoru
(*) otrzymujemy
=g(0), więc ze wzoru
(*) otrzymujemy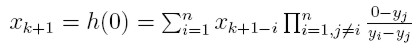
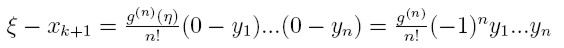
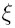 równania f(x) = 0
(Jeżeli proces iteracyjny jest zbieżny). Metoda ta polega na tym, że z
punktów
równania f(x) = 0
(Jeżeli proces iteracyjny jest zbieżny). Metoda ta polega na tym, że z
punktów 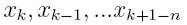 obliczamy
obliczamy 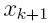 , a następnie
zastępując jeden z punktów
, a następnie
zastępując jeden z punktów 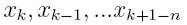 punktem
punktem 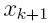 obliczamy
obliczamy 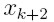 itd.
itd. jest liczbą
naturalną. Dokładnie dunkcja iteracyjna F ma rząd p <=>
jest liczbą
naturalną. Dokładnie dunkcja iteracyjna F ma rząd p <=> 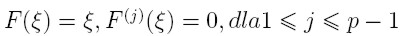 i
i