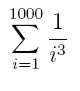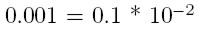
więc t = 2 , a więc 2 cyfyr poprawne
ułamkowe a więc poprawnymi liczbami są liczby: 0,01 a więc jest tylko
jedna cyfra znacząca.
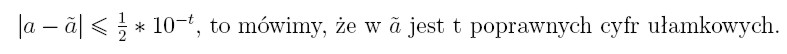
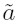 , aż do t-tej
pozycji po kropce nazywamy cyframi
znaczącymi.
, aż do t-tej
pozycji po kropce nazywamy cyframi
znaczącymi. 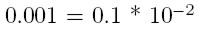
program niesk;
{$APPTYPE CONSOLE}
var x,y: single;
begin
x:=10000;
writeln(x);
y := x + 0.00001;
writeln(y);
if (x = y) then writeln('Liczby x i y są równe równe');
readln;
end.